FAQ
What is a phenotype?
Phenotypes are the expressed traits, characteristics, and diseases of an organism that arise from its DNA.What is a polygenic score?
A polygenic score (also polygenic index/predictor), is a powerful statistical tool that infers the underlying continuous genetic axis of heritable predisposition to a trait conferred by common genetic polymorphisms.Polygenic scores are the natural scientific outgrowth of the infinitesimal model of population genetics, first proposed by Ronald Fisher and Francis Galton and later confirmed by modern large-scale GWAS. The infinitesimal model postulates that complex traits are influenced by a multitude of DNA variants, each with a small effect, but that combine linearly to explain a significant fraction of individual differences within and between families.
Massive statistics on large samples of phenotyped and genotyped individuals enable us to back out estimates of these genetic effects. Quantitative prediction from DNA alone is unleashed by aggregating these genetic effects into a polygenic score: The alleles an individual carries are weighted by their estimated effects on a trait and then summed to produce the individual's estimated position relative to the population along the genetic axis. This latent genetic axis underpinning a polygenic trait is typically distributed in a Gaussian (bell curve) manner in the population owing to central limit theorem convergence.
As the cumulative size of genotyping studies grows through the 21st century, our models will converge closer on the linear genetic architecture of important heritable characteristics. In the limit, as new biobanks come online and large genotyping studies are completed with high quality phenotyping, we will map out the genomic structure of human variation with increased resolution. For some traits, we will reach the holy grail of solving the heritability. Capturing all the additive heritable information about an individual genome means we can do the equivalent of meeting the genome's identical twin from DNA alone. This has nearly occurred already for height, for which we've captured the vast majority of the total heritability.
For height and some biomarkers, we are close to saturation of the models, where we can see that additional training data yields only modest improvements in predictive performance. For nearly all other complex traits and diseases however, e.g. type 2 diabetes, prostate cancer, and breast cancer, our predictive ability is still heavily data-limited. We can see that the predictor continues to get better as the number of cases in the training increases, and this improvement shows no sign of plateauing even at the current sample size. Scaling laws provide more precise estimates, but generally you can expect our genetic effect estimates to reach convergence once the training data has about 100,000 cases for a complex disease and about 1,000,000 well-phenotyped genomes for a normally distributed quantitative trait. For almost all important phenotypes, we have not yet reached the limit of our ability to predict from DNA.
What is pleiotropy?
Pleiotropy occurs when a polymorphism in the structure of DNA influences multiple traits. A key finding of recent advances in population genetics is that pleiotropy between unrelated traits and diseases is typically diminutive. Between related traits and diseases, e.g. diseases that tend to frequently occur together, the field has found overwhelmingly synergistic pleiotropy. This means that when a change to the DNA increases the risk of one disease, it tends to also increase the risk of a related disease.In a future version of this site, you will be able to see the pleiotropy between each pair of predictors. It is expected that the multitude of traits will show a simplification and sparsity of the polygenic scores to roughly a dozen or so genetic constructs, e.g. a shared factor of cardiovascular disease liability. That is, the polygenic scores are not distributed as spheres, but rather as ellipsoids, in which the variants underlying each trait are shared with the variants underlying related traits.
How do the genetics of my annual physical measurements affect my health?
The creator of this site also trained predictors of 10-year disease risk from age, sex, and routine annual physical measurements for a wide range of common late-in-life diseases. The 26 physical measurements included things like BMI, blood pressure, and standard biomarkers, e.g., glucose, cholesterol, liver and kidney markers, and blood counts. It turns out that all of those measurements can be predicted from DNA. An obvious question is: could I predict your annual physical results from your DNA and plug them into the biometric-based disease predictors?Surprisingly, this method of stitching the output of the genes-to-biomarkers predictors to the input of the biomarkers-to-disease predictor works quite well across a range of diseases. For some diseases, e.g., non-alcoholic fatty liver disease, chronic kidney disease, it predicts disease more accurately than the regular genes-to-disease polygenic score. When there is limited training data available, it is often easier for linear models to learn about the relationship between genetics and biometrics and then separately about the relationship between biometrics and disease, as compared to regressing disease status directly on genetics, skipping the inner layer of additional biological information. For most diseases, performance improves slightly by including the biometric polygenic scores.
Using this concatenated model architecture, we can evaluate how our polygenic score for an annual physical measurement modifies overall disease risk. We take a polygenic score, e.g., for eGFR or mean arterial pressure, and estimate the change in absolute 10-year risk for some disease, e.g. coronary artery disease or hypothyroidism, at age 70 corresponding to an increase in the polygenic score by one standard deviation. We then do this for each disease and sum the effects on absolute risk. The net change in absolute risk tells us what it means to have a higher polygenic score for one of these routine physical measurements. It is the measure of the pleiotropy of a biometric polygenic score for general common disease risk. For example, we find that compared to having an average polygenic score for BMI, men with a polygenic score 1 sd above the mean have an overall greater absolute risk of any late-in-life disease by 10 percentage points.
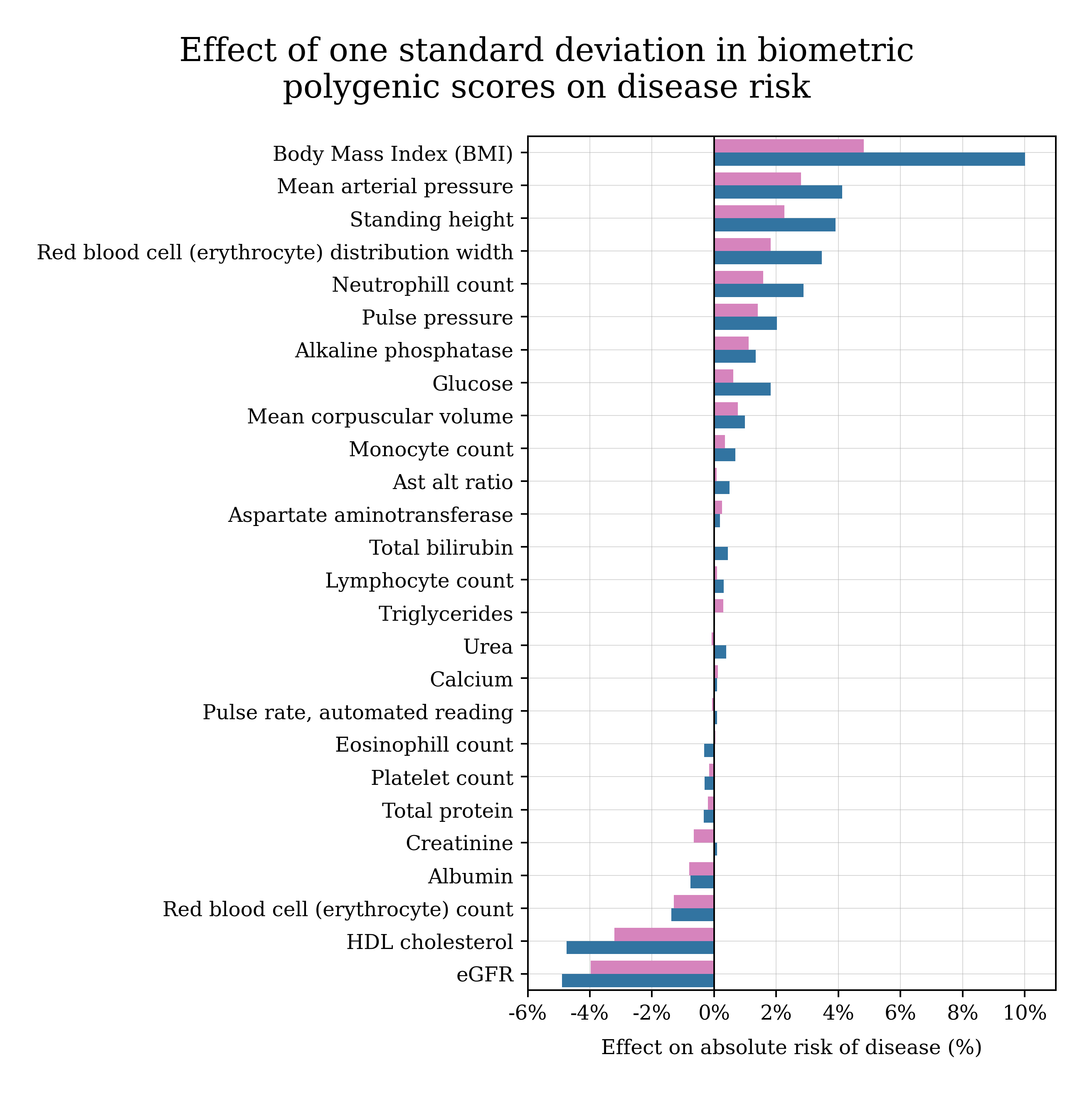
In general, we do not see trade offs in genetic predisposition to routine physical measurements. That is, we do not see situations where a high biomarker polygenic score increases risk for one disease while decreasing risk for another disease. Instead, the data suggests a pattern of synergistic pleiotropy, where genetic variants controlling a biomarker that are associated with increased risk for one disease often contribute to increased risk for other related diseases as well. This points to the existence of a genetic general factor underlying overall health: a shared genetic architecture that influences overall disease susceptibility across multiple conditions.
Interestingly, we see very little activation of pulse rate as a predictor of general disease risk and also very little activation of triglyceride levels. The latter observation might be explained by HDL cholesterol being a stronger predictor of disease risk compared to triglycerides. eGFR continues to act as a kind of biological clock for general disease risk. Kidney filtration rate declines strongly with age, and having a lower eGFR than average for your age cohort tends to come along with a higher risk of disease than average for your age cohort.
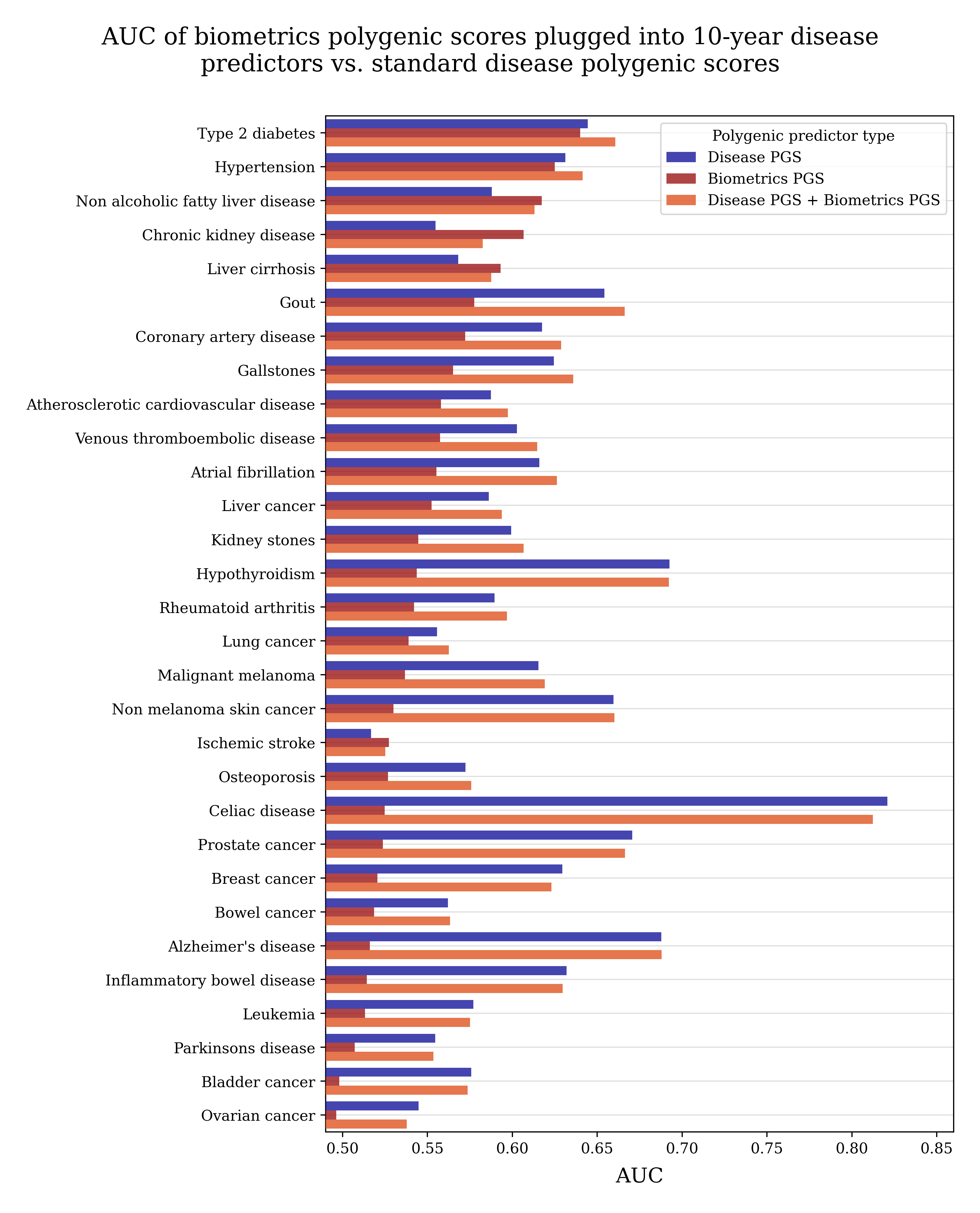
You can download the data of the estimated effects on absolute risk at age 70 by an increase by one standard deviation in the polygenic score for each biometric.
Is the genetic architecture really additive?
For those new to the field, it might appear that the additive model is merely a compromise forced by limited sample sizes. However, this assumption is incorrect. It turns out that despite strong efforts to find nonlinear genetic effects, we are failing to do so. For instance, a recent study by Kelemen et al. 2025 demonstrated through simulations that if the heritability of complex traits were primarily influenced by epistasis (interactions between genetic loci), such effects should be detectable with neural networks. However, when examining a wide range of UK Biobank phenotypes, the researchers failed to detect nonlinear genetic effects. The figure below, taken from their study, illustrates that across numerous traits and diseases in the UK Biobank, neural network models do not surpass the performance of the basic additive model.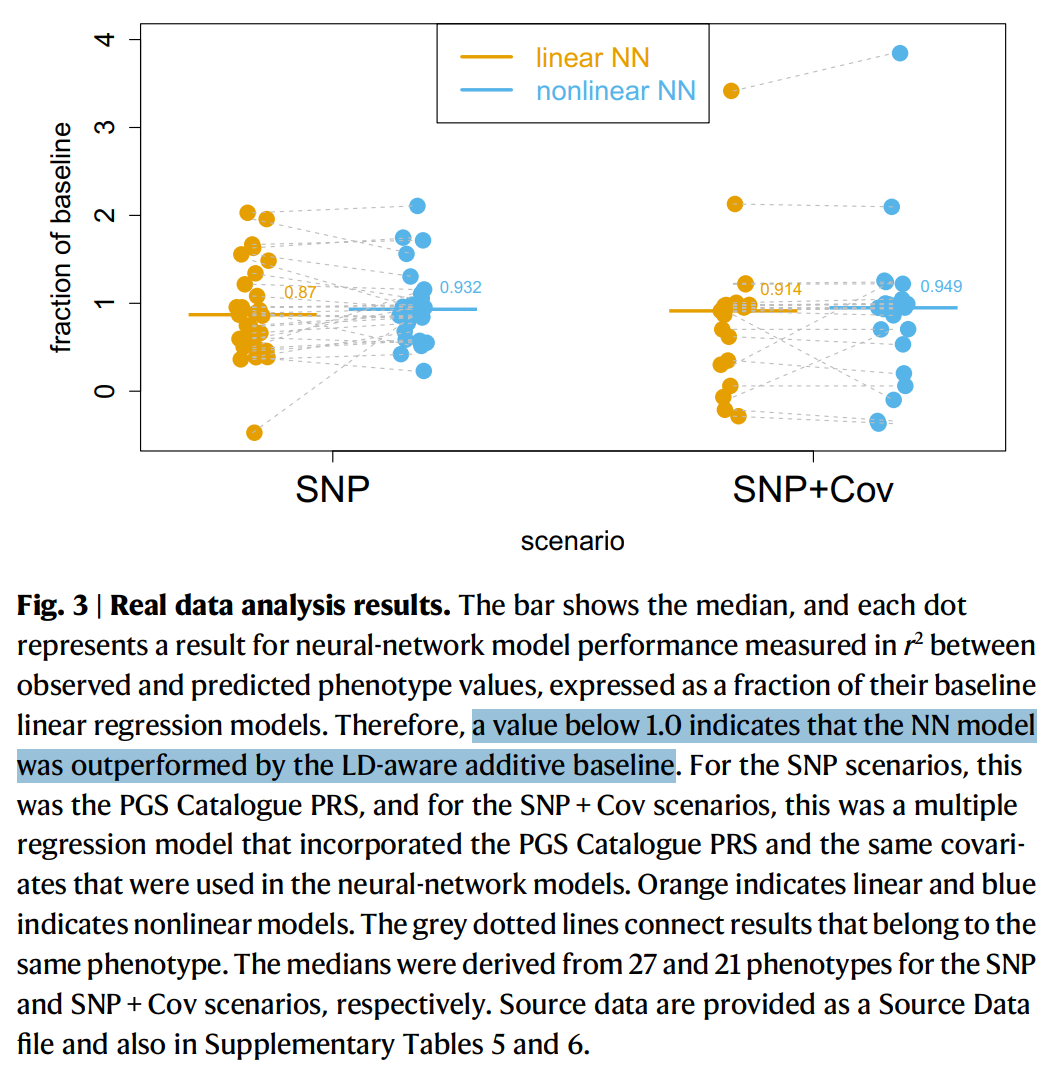
It is a very deep and important discovery of the 21st century that the genetic effects that make one individual different from another are approximately additive. This is not to say that gene x gene interactions do not occur in basic biological processes, we know that such interactions are important and can be disrupted by very rare Mendelian disorders. Rather it is to say that at the scale of common heritable differences between individuals within a population, these appear to be driven by genes acting additively within and between loci.
In light of evolution, this discovery is not so surprising. In 1930, Ronald Fisher published a differential equation that he named the fundamental theorem of natural selection, detailed in a contemporary review by Grafen (2020). It states that the rate at which a population can adapt to its environment is dominated by the amount of additive genetic variance in the population. That is, the greater the differences between members of a species controlled by additive genetic effects, the faster that species can evolve in response to selection pressure. By comparison, the speed of natural selection via nonlinear adaptations is much slower: locus-locus effects are harder to transmit to offspring because the interacting alleles are likely to break apart during meiosis.
The image below shows a pictogram of Fisher's fundamental theorem: the rate of change of average fitness over time (dF/dt) is approximately equal to the additive genetic variance (σ2A), i.e., the amount of population variance in fitness controlled by additive genetic effects. When σ2A is large (top panel), the rate of change of fitness over time is fast, and when σ2A is small (bottom panel), the rate is slow.
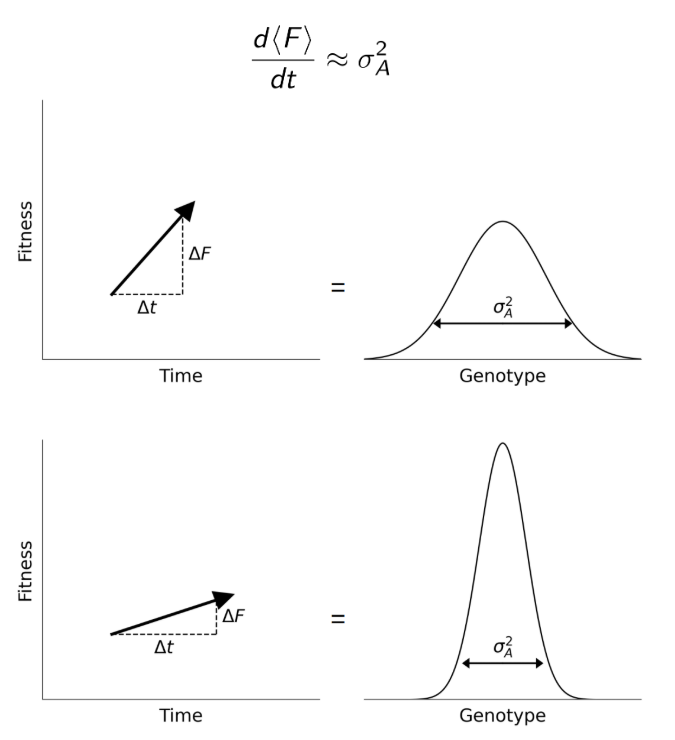
Fisher's fundamental theorem provides an evolutionary explanation for why the genetic architecture of population traits we see today is dominated by additive genetic effects. Genetic architectures that failed to adapt swiftly to environmental changes were outpaced by those that could. By the logic of natural selection, the architectures prevalent today should be those that facilitate rapid evolution, namely additive genetic architectures. Another perspective on Fisher's fundamental theorem is provided in the diagram below from Shafee (2014). It is easier to adapt modular molecular software with sparse additive features than brittle genetic code with highly interdependent components. The greater the influence of epistasis on trait variation, the slower and more challenging it is to evolve the trait.
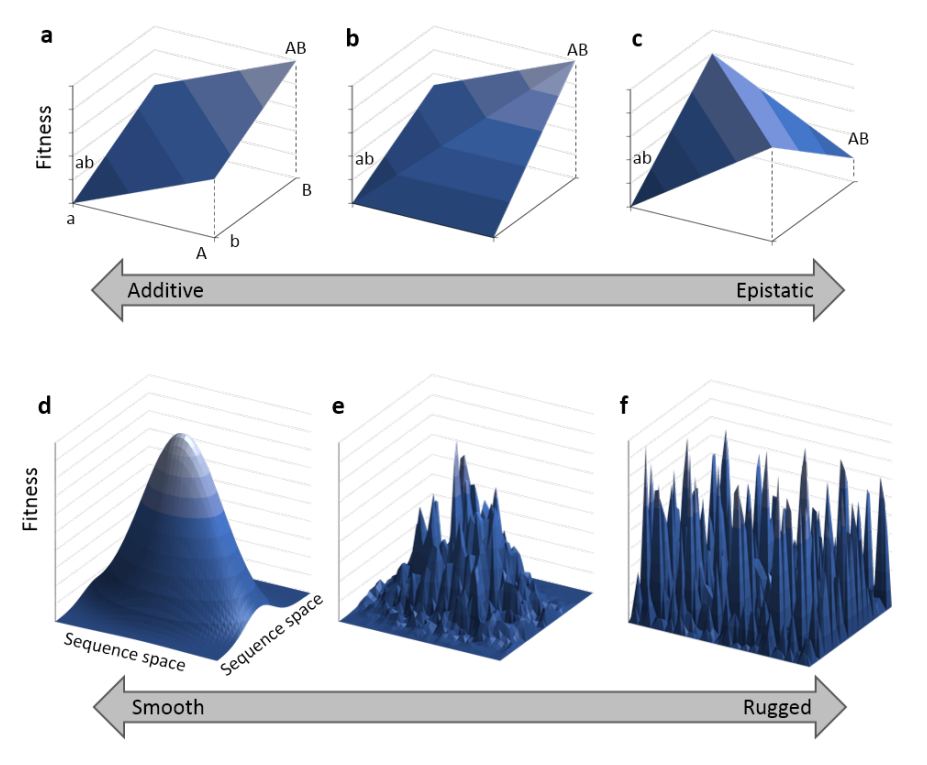
Fisher showed us that the fastest way to shift a population trait is to change the frequencies of the alleles that have additive effects. This suggests that any population trait which underwent rapid change in recent evolutionary history is likely to be underpinned by an additive genetic architecture. We can tentatively conclude that the sparse and linear genetic architecture of complex traits that we are discovering today is a product of the evolution of our ancestral lineage. We now have the chance to map out that architecture in high resolution.
Can we predict cognitive ability from DNA?
The general factor of intelligence, denoted as 'g', is a psychometric construct capturing the shared variance across various cognitive abilities. Derived from statistical analyses like factor analysis of diverse mental tasks, 'g' measures the core ability to reason, solve problems, and process information effectively. It is an extremely strong predictor of performance across a wide range of domains including job performance, income, and academic achievement.Given the significance of general intelligence, it is surprising that, in the 21st century, we have made limited progress in elucidating its genetic architecture. One might question why the NIH has not prioritized funding for a GWAS of cognitive function. The charts below demonstrate that general intelligence could be predicted from DNA as accurately as height if the necessary dataset were collected.
You can see in the chart below that as we increase the training size the predictive performance improves and that we run out of training data as we are still making linear progress in predicting the trait. This exemplifies how genetic prediction is primarily data-limited rather than algorithm-limited.
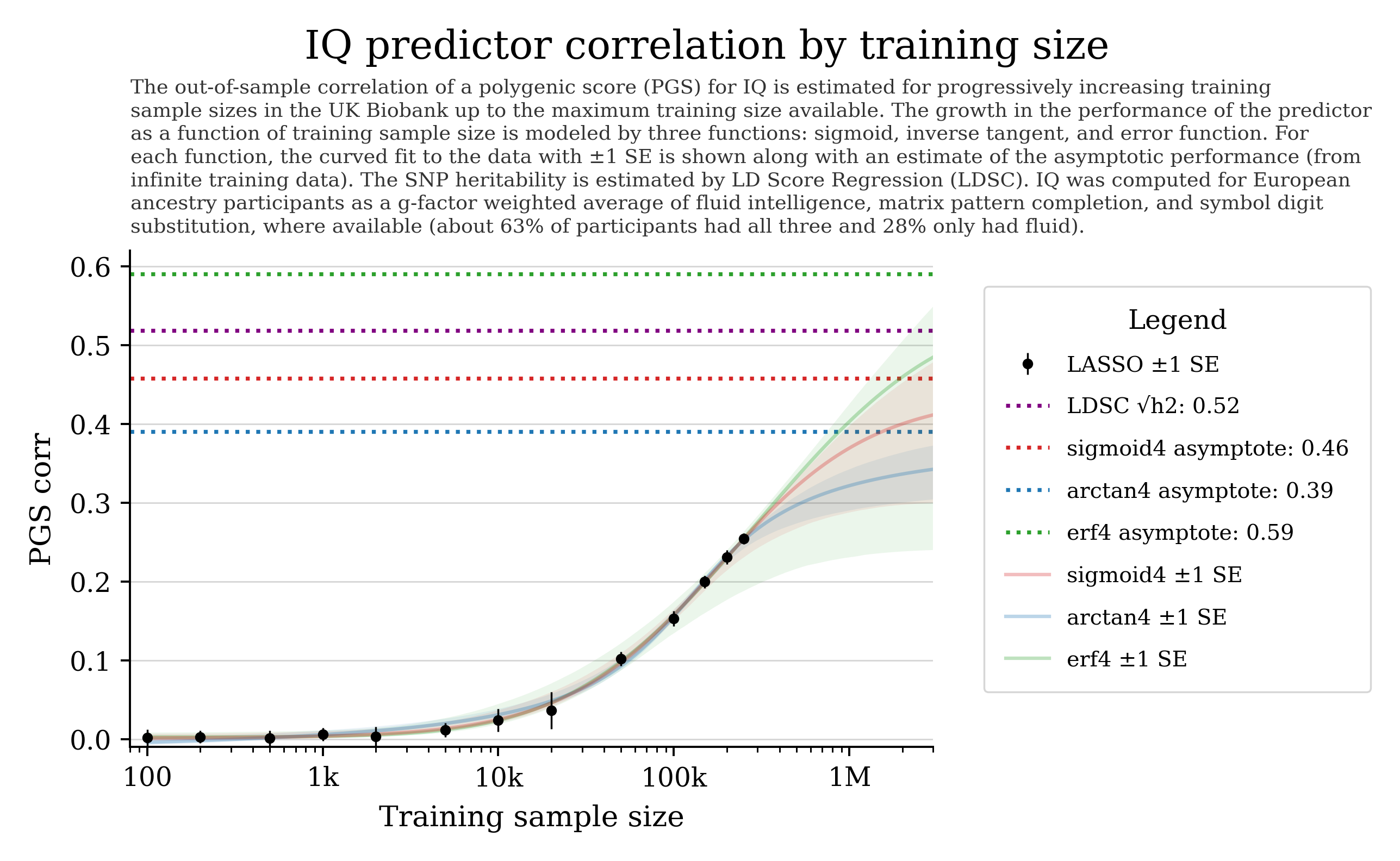
Assuming the data (IQ measurement) is generated by a linear model (additive genetics) plus noise (environment: measurement variability, incomplete heritability), compressed sensing provides guarantees on signal recovery (solving the genetic architecture) with LASSO as the sample size of the data increases.
The closest thing to a scaling law in the field of compressed sensing is the Donoho-Tanner phase transition, which says that at a threshold sample size the performance of the signal reconstruction will sharply increase then reach a plateau as the underlying model is recovered. This is a subtle point so it's worth elaborating. This means that we will see no performance even after we collect thousands of samples. Once the sample size reaches a threshold, potentially as high as 100,000 samples, predictive performance from the additive genetic model improves significantly. At this threshold, performance begins to scale roughly linearly with log sample size, until we begin to saturate the heritability of the trait measurement. We then see diminishing gains in performance with additional samples as the variance explained by our model approaches the heritability of the phenotypic measurement. The parameters governing where the phase transition occurs are the heritability of the trait and the sparsity of its genetic architecture, i.e., the number of genetic sites controlling the trait. From these parameters, there are approximate equations to estimate a priori how many samples are needed to reach the phase transition.
We can estimate the asymptotic performance of our polygenic score with infinite training data based on the estimated asymptotes of the fitting functions and the SNP-heritability of the trait (dotted purple line). The red line, which represents the sigmoid function, indicates that genotyping 2,000,000 individuals who completed the UK Biobank cognitive tests would yield a polygenic score correlation of approximately 0.4.
As you can see in the chart below, we are still making progress in the correct selection rate of the polygenic score between siblings when we run out of training data. The correct selection rate measures the ability of the polygenic score to predict which sibling scores higher on the IQ test from DNA-alone.
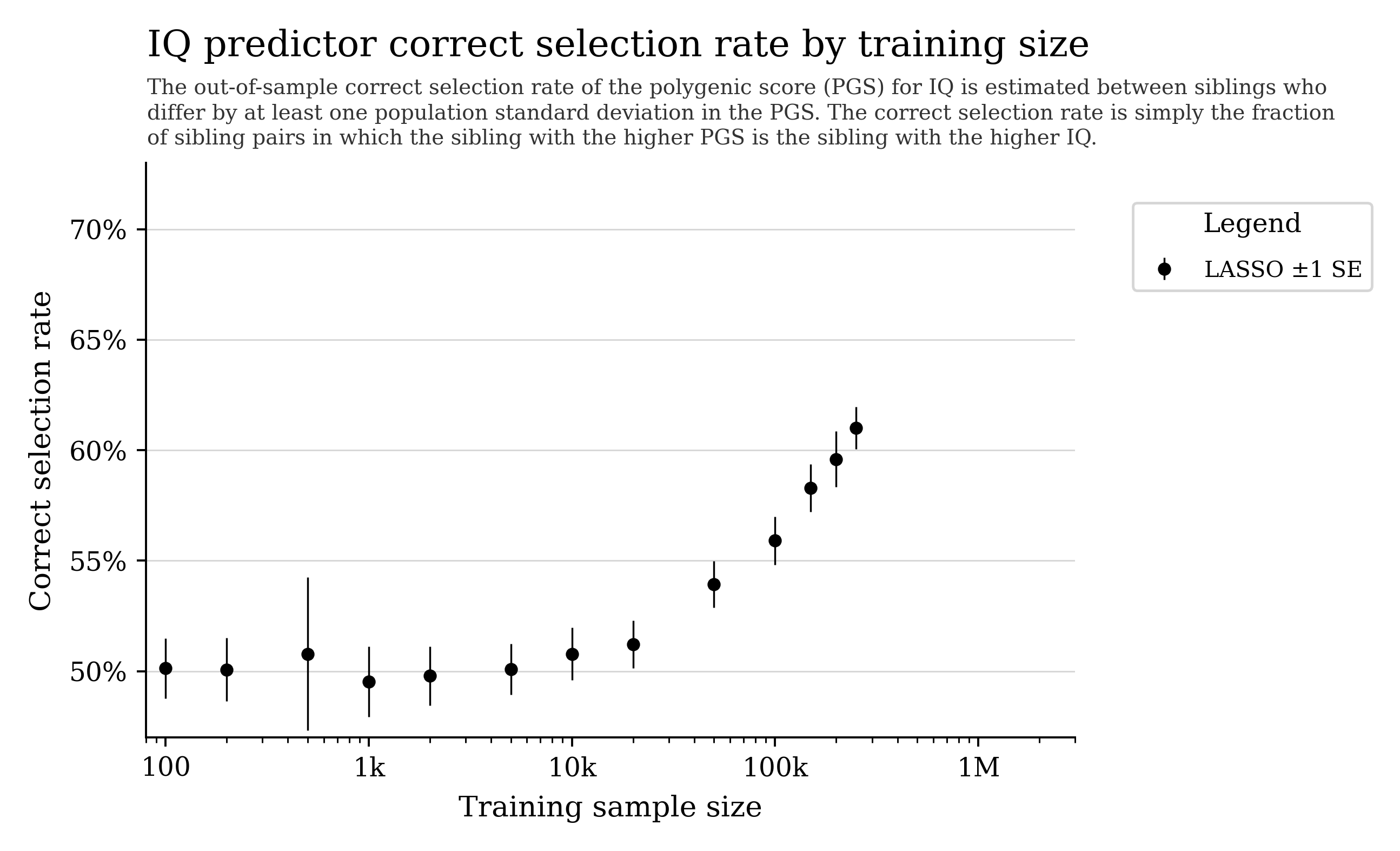
I previously suggested that we might achieve a correlation comparable to that of height (0.63 correlation). So, why do we fall short of this performance level even with a sample size of 2 million? This can be explained by the UK Biobank cognitive tests' low g-loading, which is the correlation of a test score with the general factor of intelligence. The cognitive test that most UK Biobank participants took is the fluid intelligence test, a two-minute, 13 question test of verbal and numerical reasoning. Estimating overall reasoning ability from this brief test is akin to assessing mathematical aptitude using only a two-minute segment of the SAT math section. Unsurprisingly, its g-loading is a meager 0.5, much lower than standard tests that have a g-loading of around 0.9.
This implies that we are considerably underestimating the slope of the performance curve in the chart when considering the potential growth in predictive accuracy if full-scale IQ tests were used instead. The g-loading of the test puts an upper bound on the heritability of the measurement, which forms the ceiling on the asymptotic performance we could achieve with infinite training data. Analogously, if I added a random amount between -5 and +5 centimeters to the height of each person in the UK Biobank, the heritability of the measurement would be reduced, and therefore the asymptotic performance and the slope of the training curve would be reduced. This is effectively the impact of using a test with a g-loading of 0.5, rather than a standard IQ test with a g-loading of 0.9.
Interestingly, the dataset to solve this trait already exists and is sitting in some hard drives at the Department of Veterans Affairs. The Million Veteran Program (MVP) consists of the genotypes of 1 million veterans of the U.S. military. This dataset has already been used very productively to publish GWASs of important traits like prostate cancer, malignant melanoma, HDL cholesterol, etc.
However, the MVP has neglected to run a simple GWAS of the AFQT scores of the million veterans in its dataset. Overnight, this GWAS would be better than every other IQ GWAS combined, yet it's just sitting there.
If a wealthy entity were interested in solving the genetic architecture of this phenotype, they could fund the study themselves. A standard genotype array costs about $40 per person, alternatively low-depth sequencing could be used at the cost of about $10 per person. Using participants’ historical educational test scores could eliminate the need for new testing, but such scores may have lower validity than those from newly administered tests. In total, collecting 1–2 million IQ-labeled genomes would cost between $10 million and $100 million, depending on the testing and genotyping method used. Once the dataset were collected, the genetic underpinnings of this trait could be distilled into a simple weights file, achieving an historic scientific milestone.